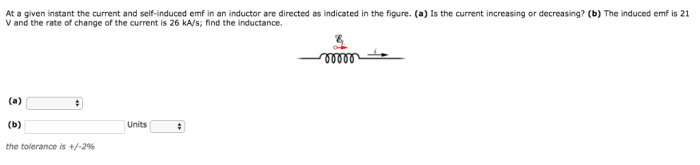
At a given instant the current and self induced emf – At a given instant, the current and self-induced EMF exhibit a dynamic relationship that shapes the behavior of electrical circuits. This article delves into the intricate interplay between these two phenomena, providing a comprehensive understanding of their fundamental concepts, mathematical underpinnings, and practical applications.
Current, the flow of electric charge, and self-induced EMF, the voltage generated by a changing magnetic field, are inextricably linked. As current flows through a conductor, it creates a magnetic field, which in turn induces an EMF that opposes the change in current.
1. Definition and Concepts

Self-induced electromotive force (EMF) is the voltage generated in a conductor due to a change in the magnetic field around it. This phenomenon occurs when an electric current flows through a conductor, creating a magnetic field. Any change in the current, such as an increase or decrease, will induce an EMF in the conductor.
The relationship between current and magnetic field is described by Ampère’s law, which states that the magnetic field around a current-carrying conductor is proportional to the current flowing through it. This means that a stronger current will produce a stronger magnetic field.
Devices that utilize self-induced EMF include transformers, inductors, and electric motors. In a transformer, self-induced EMF is used to transfer electrical energy from one circuit to another through electromagnetic induction. Inductors store energy in their magnetic field and release it when the current changes.
Electric motors convert electrical energy into mechanical energy using the principle of self-induced EMF.
2. Mathematical Analysis
The mathematical equation for self-induced EMF is given by:
$$emf =
L \fracdIdt$$
where:
- emf is the self-induced EMF in volts (V)
- L is the inductance of the conductor in henrys (H)
- I is the current in the conductor in amperes (A)
- t is the time in seconds (s)
The inductance factor (L) represents the ability of a conductor to store magnetic energy. A higher inductance indicates a greater ability to store energy.
The following table compares the self-induced EMF equations for different inductor configurations:
| Inductor Configuration | Self-Induced EMF Equation |
|---|---|
| Straight conductor | $$emf =
|
| Solenoid | $$emf =
|
| Toroid | $$emf =
|
where:
- N is the number of turns in the inductor
- μ 0is the vacuum permeability (4π x 10 -7H/m)
- A is the cross-sectional area of the inductor in square meters (m 2)
- l is the length of the inductor in meters (m)
- n is the number of turns per unit length in turns per meter (turns/m)
3. Applications and Implications
Self-induced EMF has numerous applications in electrical circuits:
- Energy storage:Inductors store energy in their magnetic field when current flows through them. This energy can be released when the current decreases.
- Power systems:Self-induced EMF plays a crucial role in power systems by limiting the flow of current and preventing short circuits.
- Transformers:Transformers use self-induced EMF to transfer electrical energy from one circuit to another through electromagnetic induction.
In real-world examples, self-induced EMF is essential for the operation of devices such as:
- Electric motors
- Generators
- Power supplies
- Electronic circuits
4. Experimental Demonstrations: At A Given Instant The Current And Self Induced Emf
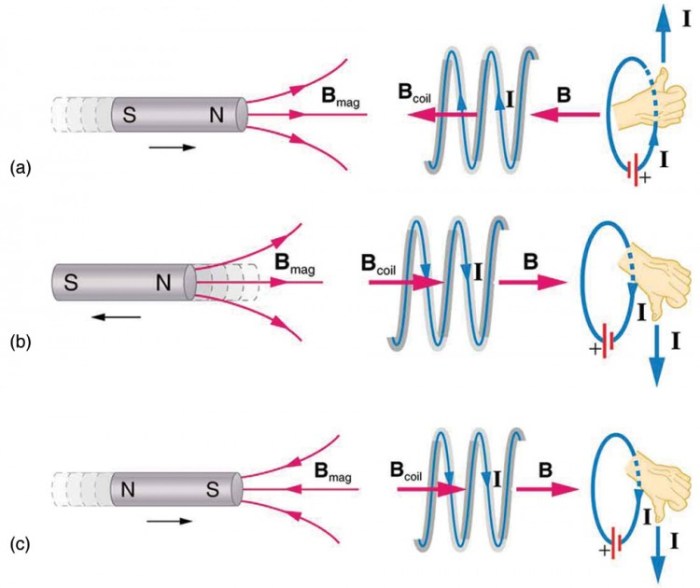
To demonstrate the presence of self-induced EMF, the following experiment can be conducted:
- Connect a battery, switch, and inductor in series.
- Close the switch and observe the current flowing through the inductor using an ammeter.
- Open the switch and observe the current again.
When the switch is closed, the current will gradually increase as the magnetic field around the inductor builds up. When the switch is opened, the current will rapidly decrease, and a voltage spike will be observed across the inductor. This voltage spike is the self-induced EMF.
5. Historical Context

The understanding of self-induced EMF evolved gradually over time:
- 1820:Hans Christian Ørsted discovered that a current-carrying wire produces a magnetic field.
- 1831:Michael Faraday discovered electromagnetic induction, which is the process by which a changing magnetic field induces an EMF in a conductor.
- 1833:Heinrich Lenz formulated Lenz’s law, which describes the direction of the self-induced EMF.
- 1851:Gustav Kirchhoff derived the mathematical equation for self-induced EMF.
Since then, the concept of self-induced EMF has been instrumental in the development of electrical engineering and has played a vital role in the advancement of modern technology.
Common Queries
What is self-induced EMF?
Self-induced EMF is the voltage generated in a conductor due to a change in the magnetic field produced by the current flowing through the conductor.
How is self-induced EMF related to inductance?
Inductance is a property of a conductor that opposes changes in current flow. It is directly proportional to the self-induced EMF generated.
What are some practical applications of self-induced EMF?
Self-induced EMF is utilized in various applications, including transformers, inductors, and electric motors.